Preclosure operator
In topology, a preclosure operator, or Čech closure operator is a map between subsets of a set, similar to a topological closure operator, except that it is not required to be idempotent. That is, a preclosure operator obeys only three of the four Kuratowski closure axioms.
Contents |
Definition
A preclosure operator on a set  is a map
is a map ![[\quad]_p](/2012-wikipedia_en_all_nopic_01_2012/I/9e6d26d0199acb41ad1ce8679db50349.png)
where 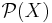 is the power set of
is the power set of  .
.
The preclosure operator has to satisfy the following properties:
![[\varnothing]_p = \varnothing \!](/2012-wikipedia_en_all_nopic_01_2012/I/2c940a4543457aa4a839f69a5db13005.png) (Preservation of nullary unions);
(Preservation of nullary unions);![A \subseteq [A]_p](/2012-wikipedia_en_all_nopic_01_2012/I/6d31c086c8911c09c12caad3b3f41e1a.png) (Extensivity);
(Extensivity);![[A \cup B]_p = [A]_p \cup [B]_p](/2012-wikipedia_en_all_nopic_01_2012/I/ace6b170ed061af0a6126b104d4ff549.png) (Preservation of binary unions).
(Preservation of binary unions).
The last axiom implies the following:
- 4.
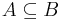 implies
implies ![[A]_p \subseteq [B]_p](/2012-wikipedia_en_all_nopic_01_2012/I/4d4aa82e429912c1cb50983b41c2bcb2.png) .
.
Topology
A set  is closed (with respect to the preclosure) if
is closed (with respect to the preclosure) if ![[A]_p=A](/2012-wikipedia_en_all_nopic_01_2012/I/1ce372df2972be7db0c24b04801b6f9a.png) . A set
. A set 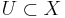 is open (with respect to the preclosure) if
is open (with respect to the preclosure) if 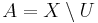 is closed. The collection of all open sets generated by the preclosure operator is a topology.
is closed. The collection of all open sets generated by the preclosure operator is a topology.
The closure operator cl on this topological space satisfies ![[A]_p\subseteq \operatorname{cl}(A)](/2012-wikipedia_en_all_nopic_01_2012/I/60ac18e93a990eca5d602c5b0a077c9a.png) for all
for all 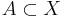 .
.
Examples
Premetrics
Given  a premetric on
a premetric on  , then
, then
is a preclosure on  .
.
Sequential spaces
The sequential closure operator ![[\quad]_\mbox{seq}](/2012-wikipedia_en_all_nopic_01_2012/I/3f196661654e75ba7503a476b26effea.png) is a preclosure operator. Given a topology
is a preclosure operator. Given a topology 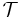 with respect to which the sequential closure operator is defined, the topological space
with respect to which the sequential closure operator is defined, the topological space 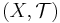 is a sequential space if and only if the topology
is a sequential space if and only if the topology 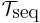 generated by
generated by ![[\quad]_\mbox{seq}](/2012-wikipedia_en_all_nopic_01_2012/I/3f196661654e75ba7503a476b26effea.png) is equal to
is equal to 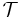 , that is, if
, that is, if 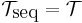 .
.
See also
References
- A.V. Arkhangelskii, L.S.Pontryagin, General Topology I, (1990) Springer-Verlag, Berlin. ISBN 3-540-18178-4.
- B. Banascheski, Bourbaki's Fixpoint Lemma reconsidered, Comment. Math. Univ. Carolinae 33 (1992), 303-309.
![[\quad]_p:\mathcal{P}(X) \to \mathcal{P}(X)](/2012-wikipedia_en_all_nopic_01_2012/I/04857e1eb8155fad436bcf40b6bf5a26.png)
![[A]_p=\{x\in X�: d(x,A)=0\}](/2012-wikipedia_en_all_nopic_01_2012/I/7c1fd6c332cbf5fb396fa1e06833a0d4.png)